
数学のテストって、いつも時間が足りなくなっちゃうんだよね〜
時間内に解き終わるにはどうしたらいいんだろう?
数学のテスト中に、一生懸命計算をしていたら時間が足りなくなってしまったという経験はありませんか?
私も高校時代、センター試験(現在の共通テスト)で時間内に解くための力をつけるのに苦労したんですよね。
実は、数学の解答スピードを上げるには単純な計算力はもちろんのこと、それ以外にも重要なことがあるんです!
今回は私がやってみて効果のあった方法も含めて、数学のテストを速く解けるようになるためのおすすめの対策をご紹介しますね♪
数学のテストで時間が足りなくなるパターンは主に3つ

まずは、なぜ数学のテストで時間が足りなくなってしまうのか、その原因を知っておきましょう。
よくありがちなパターンは、主に次の3つです。
- 基礎的な計算力が足りない
- 公式を使いこなせていない
- 文章題が苦手で時間がかかる
それぞれ、詳しくお話ししていきますね!
基礎的な計算力が足りない
「普通に計算しているつもりなのに試験で時間が足りなくなる」と感じているのであれば、単純に計算力が不足している可能性があります。
たとえば、こちらの例題は暗算で解くのが理想です。
すべて解くことはできるでしょうか?
- \( 55×11 \)
- \( 63×57 \)
- \( 125×24 \)
解答はこちら
- \( 55×11 \)
\( = 5×11×11 \)
\( = 5×121 \)
\( = 605 \) - \( 63×57 \)
\( = (60 + 3) × (60 - 3) \)
\( = 3600 - 9 \)
\( = 3591 \) - \( 125×24 \)
\( = 5×25×4×6 \)
\( = 5×100×6 \)
\( = 3000 \)
もし暗算ができなかったのであれば、計算力をアップするための対策に力を入れるのがおすすめです!
また、暗算するのは難しくても、ちょっとした工夫で計算時間の短縮&計算ミスの防止をすることも可能です。
こちらの例題で、それを体感することができるかと思います。
- \( 126×12 - 133×9 \)
解答はこちら
- \( 126×12 - 133×9 \)
\( = 2×7×9×12 - 7×19×9 \)
\( = (2×12 - 19)×7×9 \)
\( = 5×7×9 \)
\( = 315 \)
計算力を強化してなるべく暗算で答えを出せるようになれば、解答スピードは一気に上がりますよ。
「単なる計算」とあなどらずに、地道な努力を怠らないようにしましょうね!
公式を使いこなせていない
数学って、いろんな公式が登場して覚えるだけでも大変ですよね…。
また、覚えたはいいもののどうやって使えばいいのかわからない、ということもあるかもしれませんね。
しっかりと対策をすれば、問題を見てすぐにどの公式を使えばいいのか判断することができるようになるのですが、経験や理解が不足していれば公式を使いこなすことは難しいでしょう。
まずは公式を正しく覚えることが重要ですが、テストで使いこなせるようになるためには演習も欠かせません。
文章題が苦手で時間がかかる
「単純な計算問題はできるのに、文章題になると問題文を理解するのに時間がかかる…」
こういった悩みを抱える生徒さんも、少なくありません。
私も問題の冒頭に長い文章が書かれてあると、ちょっとイヤだな~と思ってしまいます(苦笑)
学校の定期テストなら計算のみの問題の割合も高いかもしれませんが、入試では文章題は必ずと言っていいほど出題されます。
文章題の場合意地の悪いひっかけ問題も作りやすいので、出題されるのはある意味当然なんですよね。
入試では、文章題で得点できるかどうかが合否のカギになることも珍しくありません。
問題文を少しでも早く正確に読み解くことができれば、時間の余裕が生まれて計算の凡ミスを減らすことも期待できますよ。
数学の解答スピードを上げるためにやるべき勉強法
数学のテストで時間が足りなくなるパターンを3つお話ししましたが、気になるのはどうやったら時間内に解けるようになるのか?ということですよね。
解決するためには、どのパターンが自分に最も当てはまっているのか、分析をして対策することが大切です!
原因別に、具体的な対策方法をご紹介しますね。
基礎的な計算力をアップしたいなら地道な努力を続けよう!
基礎的な計算力が不足しているなら、まずは何よりも先に対策をすべきです!
おすすめの対策は、問題集を使って単純な計算問題を繰り返し演習することです。
こんなことをして意味があるの?って思うかもしれませんが、野球選手が毎日バットを素振りするのと同じように、数学でも毎日地道な計算練習を繰り返すことで基礎的な計算力が上がります!
私も、入試直前期には朝ご飯を食べる前に百ます計算をやることを日課にしていました。
センター試験の数学で満点を取ることができたのも、この毎日の積み重ねで計算力を高めていたからだと思っています。
1回5分もかからないので、ぜひ今日から取り入れてみてください♪
さらにこちらの参考書も活用すれば、テクニックも鍛えることができます。
「意外と知らないことが多かった!」「わかっていたつもりだったけど、実はきちんと理解できていなかった!」という内容もあるかもしれませんので、ぜひ手に取ってみてくださいね。
公式を覚えたら使いこなすための対策をしよう!
公式はまずしっかりと覚えることが大切ですが、それだけではテストの点数に結びつきません。
公式を使いこなして、いち早く答えにたどり着くことが高得点のカギになるんです!
ある問題を見て、どの公式を使えばいいのかすぐに判断できるようになるためには、何度も演習を繰り返して、経験を重ねることが必要です。

な~んだ!!
これさえ知っておけばスラスラと解けるようになる、みたいな神ワザがあるかと思ったのに~!!
ちょっとガッカリしたかもしれませんが、瞬時に公式を使いこなせるようになる魔法みたいなものがあれば誰も苦労しないですよね(笑)
ただし、正しい努力をすることで力を伸ばす速度を上げることはできますよ!
例えば、以下の参考書を使ってみるのがおすすめです。
公式を詳しく解説している参考書を活用しながら、たくさんの問題演習をこなすことで着実にレベルアップすることができるはずです。
1つ1つをしっかりと理解して、テストで使いこなせるようになりましょうね!
文章題は数式や図に置き換えて考えよう!
文章題を速く解くコツは、文章を数式や図に置き換えることです!
こちらも、例題を一緒に見てみましょう。
Aくんの年齢を3倍して4足すと、Aくんのお父さんの年齢と同じになります。
Aくんのお姉さんの年齢を3倍して4引くと、Aくんのお母さんの年齢と同じになります。
Aくんのお父さんは、Aくんのお母さんより2歳年上です。
AくんとAくんのお姉さんは、何歳離れていますか?
解答はこちら
Aくんの年齢を\(x \)、Aくんのお姉さんの年齢を\(y \)とする。
このとき、Aくんのお父さんの年齢は\( 3x + 4 \)、お母さんの年齢は\( 3y - 4 \)と表される。
したがって、お父さんの年齢からお母さんの年齢を引くと2になるので、
\( (3x + 4) - (3y - 4) = 2 \)
となる。
これを解くと、
\( (3x + 4) - (3y - 4) = 2 \)
\( 3x + 4 -3y + 4 = 2 \)
\( 3x -3y = -6 \)
\( y - x = 2 \)
以上より、AくんとAくんのお姉さんは2歳離れている。
Aくんたちの年齢の関係をグラフで表すと、次の通りとなる。
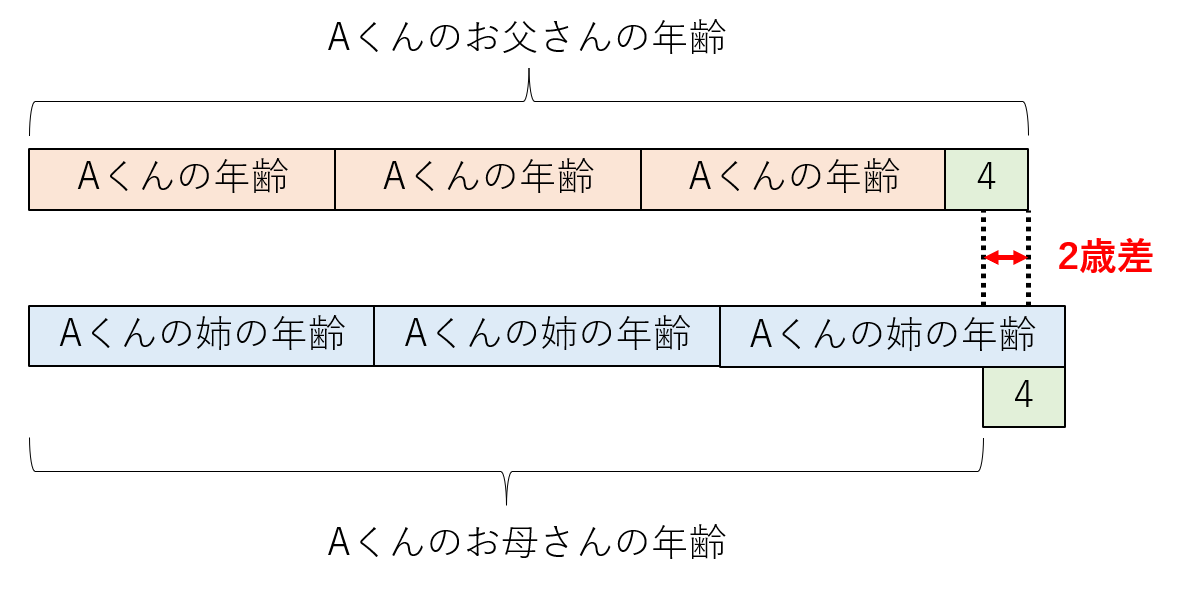
いかがですか?
簡単な例題ではありますが、文章のまま考えるよりも数式や図で考える方がわかりやすくなると実感できたのではないでしょうか?
もっとレベルの高い大学入試問題でも、根本的な解き方は同じです。
落ち着いて文章を読み、自分で数式や図を考える練習をすることで、問題をより速く正確に解けるようになるはずですよ!
最初はうまくいかないかもしれませんが、意識して取り組むことでだんだんできるようになってくると思います。
コツを掴めるまで、粘り強く演習してみてくださいね♪
まとめ
- 数学のテストで時間が足りなくなるのは、「基礎的な計算力が足りない」「公式を使いこなせていない」「文章題が苦手で時間がかかる」の3つのパターンがある
- 「基礎的な計算力が足りない」場合は、単純な計算問題を繰り返し解いたり、解答スピードアップに役立つ参考書を活用したりするとよい
- 「公式を使いこなせていない」場合は、公式の理解を深めるための参考書を読みながら、問題演習をこなすことで着実にレベルアップできる
- 「文章題が苦手で時間がかかる」場合は、文章を数式や図に置き換えるように意識しながら問題演習に取り組むとよい
ご紹介した対策を取り入れて勉強すれば、きっと数学のテストで時間内に解き切れるようになるはずです!
テストの成績アップや志望校合格を実現できるように、応援しています♪









